僥僽僫儞偺掕棟
僥僽僫儞偺掕棟偲偼
僥僽僫儞偺掕棟偼丄僉儖僸儂僢僼偺朄懃偱夝偔偲帪娫偑偐偐傞応崌偵栶棫偪傑偡丅
恾1偺夞楬偱偙偺掕棟傪峫偊傑偡丅
恾1
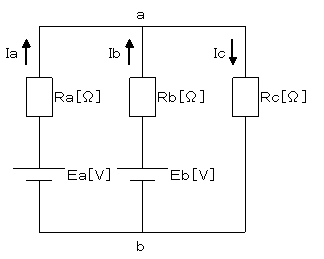
恾2偼丄恾1偺敿暘偐傜嵍懁偺夞楬傪愗傝偲偭偨恾偱偡丅
恾2
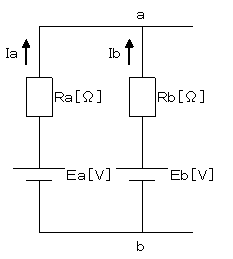
恾2傪娙扨偵偡傞偨傔恾3偵曄宍偟傑偡丅
恾3
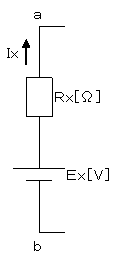
恾2偺夞楬偼丄Ra偲Rb偑暲楍偵側偭偰偄傑偡偺偱丄a-b娫偺掞峈Rx偼丄
Rx=Ra亊Rb/Ra亄Rb丂丒丒丒嘆
揰b偐傜帪寁夞傝偵僉儖僸儂僢僼偺朄懃傪揔梡偡傞偲丄
Ea-IaRa亄IbRb-Eb=0丂丒丒丒嘇
恾傛傝
Ib=-Ia丂丒丒丒嘊
嘊傪嘇偵戙擖偡傞偲丄
Ea-IaRa亄IbRb-Eb=Ea-IaRa-IaRb-Eb
=Ea-Ia(Ra亄Rb)-Eb=0丂丒丒丒嘋
嘋傪曄宍偡傞偲丄
Ea-Ia(Ra亄Rb)-Eb=0
Ea-Eb=Ia(Ra亄Rb)
Ia=(Ea-Eb)/(Ra亄Rb)丂丒丒丒嘍
a-b娫偺揹埑Ex偼丄b揰偐傜Ea丄Ra傪捠傝a揰傊Ia偑棳傟偰偄傞偺偱
Ex=Ea-IaRa
=Ea-(Ea-Eb)Ra/(Ra亄Rb)丂丒丒丒嘐
嘆偲嘐傛傝丄僥僽僫儞偺掕棟傪揔梡偡傞偲丄恾1偼恾3偺傛偆偵曄宍偱偒傑偡丅
恾3
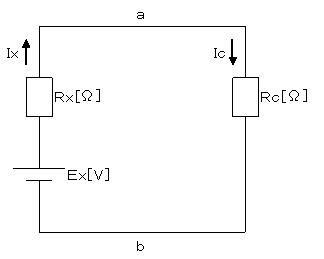
Rx=Ra亊Rb/Ra亄Rb
Ex=Ea-(Ea-Eb)Ra/(Ra亄Rb)
僥僽僫儞偺掕棟偺巊偄曽
亙椺戣亜
壓恾偺傛偆側丄6[V]偲8[V]偺揹抮丄3[兌]偲4[兌]偲12[兌]偺掞峈偐傜側傞夞楬偑偁傞丅
Ic傪媮傔傛丅
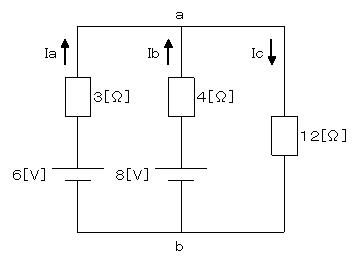
僥僽僫儞偺掕棟傛傝
Rx=Ra亊Rb/Ra亄Rb丂丒丒丒嘆
Ex=Ea亄(Ea-Eb)Ra/(Ra亄Rb)丂丒丒丒嘇
嘆偵掞峈3[兌]偲4[兌]傪戙擖偡傞偲丄
Rx=Ra亊Rb/Ra亄Rb=3亊4/3亄4=12/7
嘇偵掞峈3[兌]偲4[兌]丄揹埑6[V]偲8[V]傪戙擖偡傞偲丄
Ex=Ea-(Ea-Eb)Ra/(Ra亄Rb)
=6-乷(6-8)亊3乸/(3亄4)
=6-(-6)/7
=48/7
傛偭偰椺戣偺恾偼壓恾偺傛偆偵曄宍偱偒傞丅
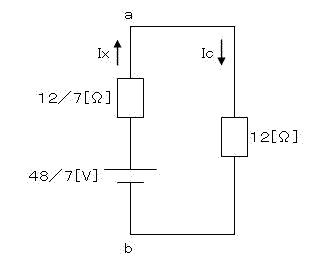
偙偺恾傛傝
Ic=E/R
=(48/7)/(12/7亄12)
=(48/7)/(12/7亄84/7)
=(48/7)/(96/7)
=48/96
=0.5[A]
摎偊丂Ic=0.5[A]
TOP儁乕僕偵栠傞
僒僀僩撪専嶕
揹婥偲偼側偵偐
揹婥偺楌巎
揹壸
揹婥椡慄偲揹懇
尨巕偲暘巕偲揹巕
揹婥偺夞楬偲悈偺夞楬
揹棳偲偼
揹埑偲偼
掞峈偲偼
揹椡偲揹椡検
捈楍丒暲楍愙懕偺崌惉掞峈
暘埑偲暘棳
捈棳偲岎棳
惓尫攇岎棳
掞峈丒儕傾僋僞儞僗丒僀儞僺乕僟儞僗
揹奅偲帴奅
帴壸
帴椡慄偲帴懇
帴婥僸僗僥儕僔僗
僐僀儖偲僀儞僟僋僞儞僗
僐儞僨儞僒偲惷揹梕検
嫟怳
椡棪偲旂憡丒桳岠丒柍岠揹椡
楇憡揹棳偲I0r丒I0c
3憡岎棳
儀僋僩儖恾偺巊偄曽
揹慄偵偲傑偭偨捁偑姶揹偟側偄棟桼
廀梫棪偲晧壸棪偲晄摍棪
僷乕僙儞僩僀儞僺乕僟儞僗朄(亾Z)
儂僀乕僩僗僩儞僽儕僢僕
僗僞乕僨儖僞曄姺丒僨儖僞僗僞乕曄姺
揹埑崀壓
夁搉尰徾
夁搉尰徾(R-L捈楍夞楬)
夁搉尰徾(R-C捈楍夞楬)
尨巕椡敪揹偺巇慻傒
悈椡敪揹偺巇慻傒
壩椡敪揹偺巇慻傒
懢梲岝敪揹偺巇慻傒
娭搶偲娭惣偱廃攇悢偑堘偆棟桼
側偤岎棳憲揹側偺丠
掆揹
弖帪揹埑掅壓
庴揹曽幃
僗億僢僩僱僢僩儚乕僋庴揹曽幃偺巇慻傒
儖乕僾庴揹曽幃偺巇慻傒
恑憡僐儞僨儞僒偲椡棪妱堷
幷抐婍偲奐暵婍偲抐楬婍
奐暵僒乕僕
GIS(僈僗愨墢奐暵憰抲)
UGS丒UAS丒PGS丒PAS
曐岇宲揹婍
曄埑婍(僩儔儞僗)
椼帴撍擖揹棳
愙抧(傾乕僗)
摑崌愙抧
愙抧梡曗彏僐儞僨儞僒
揹尮忕挿壔
僼僃儔儞僠岠壥
僆乕儉偺朄懃
僋乕儘儞偺朄懃
僉儖僸儂僢僼偺朄懃
僼傽儔僨乕偺朄懃丒儗儞僣偺朄懃
僼儗儈儞僌偺朄懃
儈儖儅儞偺掕棟
僥僽僫儞偺掕棟
僈僂僗偺掕棟
廳偹崌傢偣偺棟
傾儞儁傾廃夞愊暘偺朄懃
價僆丒僒僶乕儖偺朄懃
戞3庬揹婥庡擟媄弍幰 棟榑
戞3庬揹婥庡擟媄弍幰 揹椡
戞3庬揹婥庡擟媄弍幰 婡夿
戞3庬揹婥庡擟媄弍幰 朄婯
戞2庬揹婥庡擟媄弍幰 1師棟榑
戞1庬揹婥庡擟媄弍幰 1師棟榑
戞1庬揹婥庡擟媄弍幰 1師揹椡
戞1庬揹婥庡擟媄弍幰 1師婡夿
戞1庬揹婥庡擟媄弍幰 1師朄婯
戞1庬揹婥庡擟媄弍幰2師帋尡 揹椡丒娗棟
戞1庬揹婥庡擟媄弍幰2師帋尡 婡夿丒惂屼
僄僱儖僊乕娗棟巑(揹婥) 揹婥偺婎慴
媄弍巑堦師帋尡 嫟捠壢栚悢妛
媄弍巑堦師帋尡 嫟捠壢栚暔棟
媄弍巑堦師帋尡 嫟捠壢栚壔妛
媄弍巑堦師帋尡 婎慴壢栚
媄弍巑堦師帋尡 揹婥揹巕晹栧 愱栧壢栚
媄弍巑堦師帋尡 揔惈壢栚
媄弍巑擇師昅婰帋尡 揹婥揹巕晹栧 昁恵壢栚
媄弍巑擇師昅婰帋尡 揹婥揹巕晹栧 慖戰壢栚 敪憲攝曄揹
媄弍巑擇師昅婰帋尡 揹婥揹巕晹栧 慖戰壢栚 揹婥墳梡
媄弍巑擇師昅婰帋尡 揹婥揹巕晹栧 慖戰壢栚 揹巕墳梡
媄弍巑擇師昅婰帋尡 揹婥揹巕晹栧 慖戰壢栚 忣曬捠怣
媄弍巑擇師昅婰帋尡 揹婥揹巕晹栧 慖戰壢栚 揹婥愝旛
媄弍巑擇師昅婰帋尡 憤崌媄弍娔棟晹栧 昁恵壽栚
