ガウスの定理

ガウスの定理とは

電荷と電気力線の関係

任意の閉曲面から出て行く電気力線の総数は、その閉曲面に含まれる電荷の総和の1/εになります。これをガウスの定理といいます。εは電荷周囲の媒質の誘電率です。

電気力線密度とは

単位面積当たりの電気力線の本数を電気力線密度といいます。
電気力線密度の求め方を考えてみます。
図1は、半径r[m]の球殻の中に電荷q[C]を置いた図です。
図1

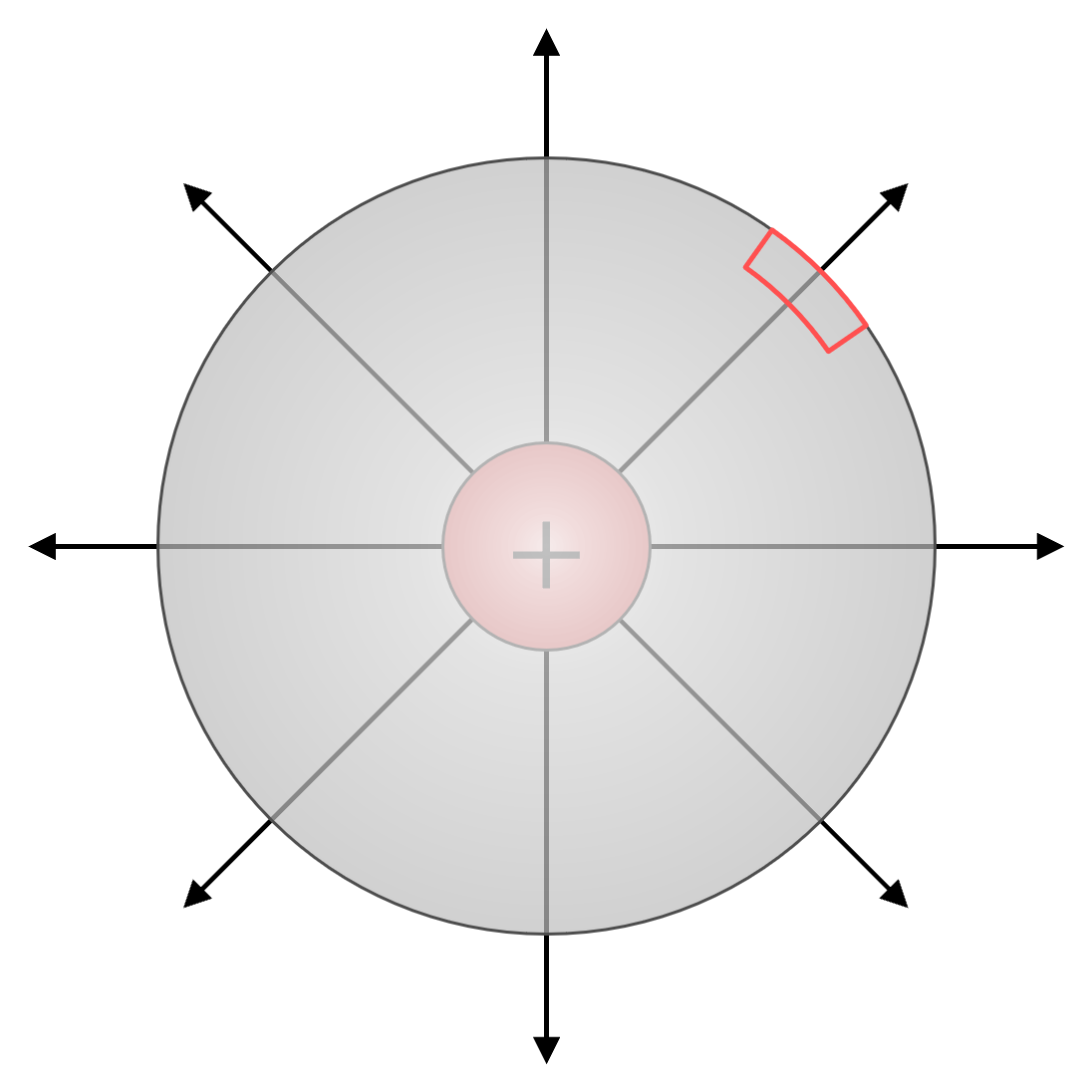
ガウスの定理より、電荷から出ている電気力線の総数をN[本]、球殻の中の電荷をq[C]、誘電率をεとすると

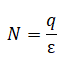
が成立します。つまり、球殻の中の電荷からはq/ε[本]の電気力線が出ています。

電荷からr[m]の位置における電気力線密度は、球殻の中の電荷から出ている電気力線の総数を、球殻の面積で割れば求められます。

半径r[m]の球殻の面積はS=4πr2なので、電気力線の総数N[本]を球殻の面積S�uで割ると

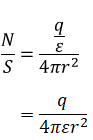
となります。

電界の強さ

任意の面1[�u]を垂直に通過する電気力線の本数が電界の強さと等しくなります。
つまり図1において、電気力線密度は電界の強さE[V/m]と等しくなります。
したがって、電界の強さE[V/m]は

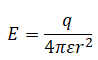
で求めることができます。

TOPページに戻る
サイト内検索