正弦波交流

正弦波交流の特徴

正弦波交流とは

正弦波交流は、グラフ1のような波形を描く交流をいいます。
グラフ1

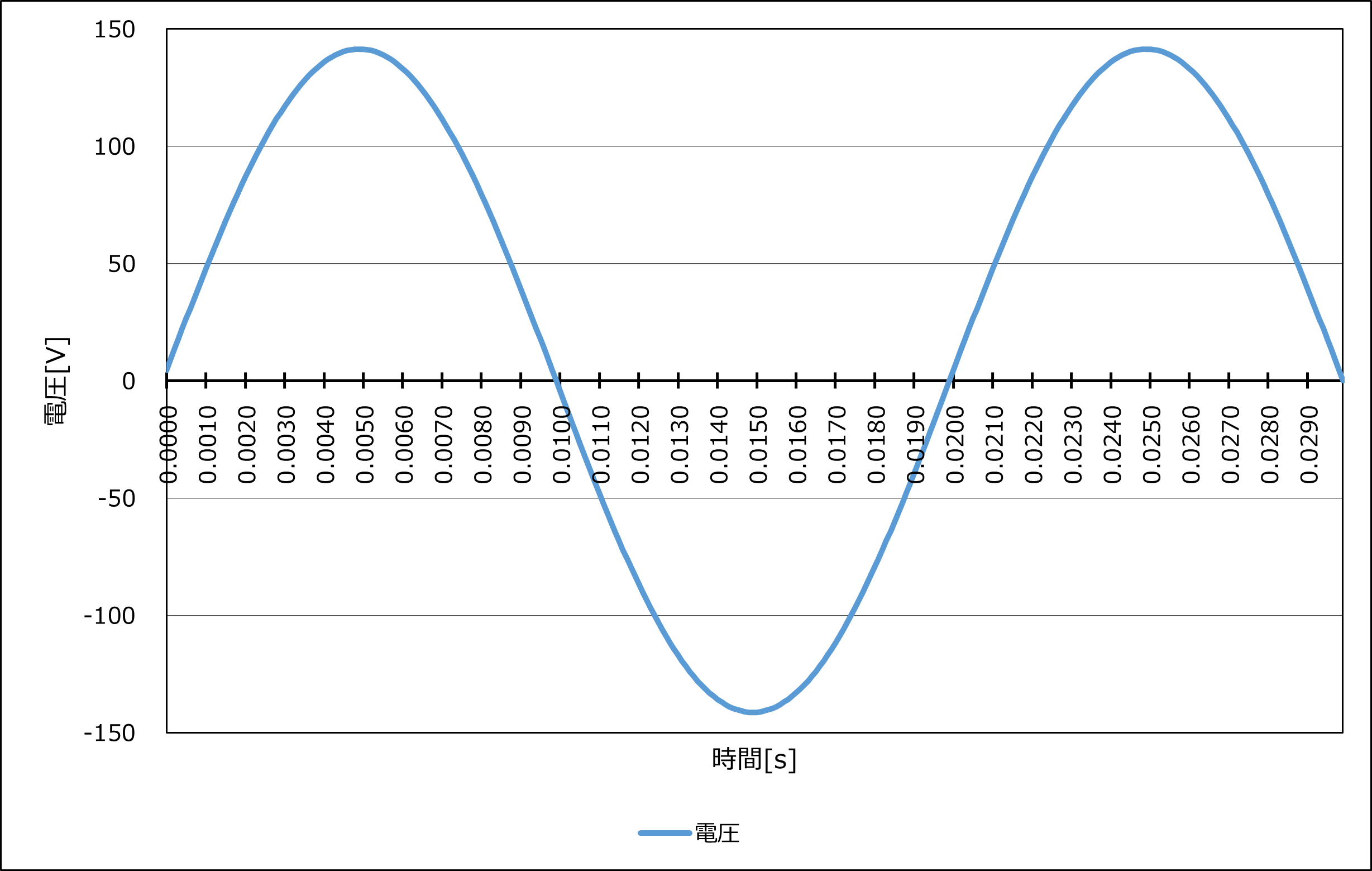
グラフ1は、縦軸を電圧、横軸を時間として正弦波交流の電圧を描いています。
電力会社から供給される電力も正弦波交流です。

周期

グラフ1の時間0.000[s]から0.020[s]までの、山が1つ、谷が1つの時間を周期やサイクルといいます。よってグラフ1は1周期分(1サイクル分)の波形ということになります。

周波数

周波数とは

1秒間に＋から-に切り替わる回数を周波数と言い、単位はHz(ヘルツ)です。1Hzは1秒間のうち0.5秒は＋、残りの0.5秒は-ということになります。
周波数をf[Hz]、周期をT[s]とすると、
f=1/T
が成り立ちます。グラフ1は周期が0.020[s]なので、周波数fは、
f=1/T
=1/0.020
=50
となり、50[Hz]の正弦波交流であることがわかります。

電力会社で用いられている商用周波数

電力会社が供給する電力の周波数を商用周波数といいます。日本では、静岡県の富士川から新潟県の糸魚川あたりを境にして、東側が50Hz、西側が60Hzの商用周波数が用いられていますので、東京は50Hzの電力が電力会社から供給されています。
50Hzは1秒間に50サイクルですから、50個の＋と50個の-が交互に入れ替わります。1秒間に＋と-が50個ずつということは1秒÷50Hz÷2=0.01秒ごとに＋と-が入れ替わることになります。 初めの0秒から0.01秒までが＋で、0.01秒から0.02秒までが-というふうに、規則的に変化します。

瞬時値

瞬時値と瞬時式

直流100Vは、常時100Vぴったりの電圧が＋-が入れ替わることがありません。しかし正弦波交流は、＋と-が交互に入れ替わります。そして、グラフ1を見ればわかるように、＋の期間も-の期間も瞬間の電圧は一定ではなく、刻々と変化し続けます。100Vの正弦波交流の場合、＋の期間では0〜141.2V、-の期間では-141.2〜0Vまで変化しています。その瞬間、瞬間の値を瞬時値といいます。
電圧の瞬時値をV[V]、電圧の最大値をVm[V]、周波数f[Hz]、時間をt[s]とすると、正弦波交流の瞬時電圧Vは
V=Vmsin2πft
瞬時電流Iは
I=Imsin2πft
となります。これを瞬時式といいます。

実効値

実効値とは

「家庭のコンセントの電圧は100V」といいますが、この100Vというのは実効値です。
交流100Vというのは正確に言うと「電圧の実効値が100Vの交流」です。

なぜ実効値で表すのか

交流の100[V]1[A]と、直流の100[V]1[A]をエネルギー的に等価にしないと、交流の100Wのヒーターと、直流の100Wのヒーターでは発生する熱が異なってしまうといった不都合が生じます。交流の100[V]1[A]と、直流の100[V]1[A]をエネルギー的に等価にした場合、交流の100[V]は電圧の実効値、1[A]は電流の実効値といいます。

直流と交流をエネルギー的に等価にする方法

抵抗R[Ω]のヒーターを直流電源に接続した場合、直流電流をId[A]、通電時間をT[s]とすると、消費される電力量Wd[Ws]は、
Wd=Id²RT
となります。
しかし抵抗R[Ω]のヒーターを交流電源に接続した場合は少々厄介です。電流は刻々と変化しますので、瞬間、瞬間で電力を計算し、通電時間T[s]分合計しなければいけません。
しかし簡単に計算する方法があります。簡単な例で説明します。
抵抗R[Ω]のヒーターを直流電源に接続した場合、直流電流をId[A]、通電時間をT[s]とすると、消費される電力量Wd[Ws]は
Wd=Id²RT
で求められます。
ここでRを2[Ω]とし、直流電流Idが
0〜1[s]までが2[A]
1〜2[s]までが3[A]
2〜3[s]までが4[A]
というように変化したとします。
0〜1[s]までに消費される電力W1は
W1=I²RT
=2²×2×1
=8
以下同様に
1〜2[s]までに消費される電力W2は
3²×2×1
=18
2〜3[s]までに消費される電力W3は
4²×2×1
=32
よって0〜3[s]までに消費される電力は
W1＋W2＋W3
=8＋18＋32
=58[Ws]
となります。
これを別の方法で計算してみます。
まず0〜3[s]の間の電流の2乗の平均値を求めます。
(2²＋3²＋4²)/3
=(4＋9＋16)/3
=29/3
そして電流の2乗の平均値にR=2[Ω]とT=3[s]をかけます。
(29/3)×2×3
=58[Ws]
となり、当たり前ですが同じ値が導かれます。
この変化する直流電流を交流電流と考えると、交流電流瞬時値を2乗して抵抗Rをかけたものを0〜T[s]分合計するということは、交流電流瞬時値の2乗の平均値に抵抗RとT[s]をかけたものと等しいということです。
よって交流電流の瞬時値をIa[A]、通電時間をT[s]とすると、消費される電力量Wa[Ws]は、
Wa=(Ia²の平均値)RT
となります。
直流の電力量Wdと交流の電力量Waを等価にするためには、
Wd=Wa
が成立しなければいけないので
Wd=Wa
Id²RT=(Ia²の平均値)RT
Id²=Ia²の平均値
Id=√(Ia²の平均値)
より、交流電流の瞬時値Ia[A]の2乗の平均値の平方根が、直流電流Id[A]と等しくしなければいけません。
交流電流の瞬時値の2乗の平均値の平方根を実効値といいます。
交流電流の瞬時値Ia[A]の瞬時式を
Ia=Imsin2πft
とすると、交流電流の瞬時値Iaの2乗は、
Ia²=Im²sin²2πft
sin²θ=(1-cos2θ)/2なので
Ia²=Im²(1-cos4πft)/2
となります。cos4πftの平均は0なので
(Ia²の平均)=Im²/2
Im²=2(Ia²の平均値)
Im=√2×(Ia²の平均値の平方根)
=√2×実効値
となります。よって実効値の√2倍が最大値になることがわかり、交流電流の瞬時値Ia[A]の瞬時式を
Ia=Imsin2πft
=Ir√2sin2πft
と変形することができます。
電圧の瞬時式も同様に
V=Vmsin2πft
=Vr√2sin2πft
と変形できます。
sin2πftはfとtの値によって変化しますが、最小は0、最大はsin2πft=1です。よって交流電圧の最大値はVr√2、つまり実効値の√2倍となります。グラフ1を見ると、一番高いところが100Vの√2倍である、141.2Vくらいを示しているのがわかります。

√2の理由

交流の最大値が√2倍である理由を違う視点で見てみます。
グラフ2

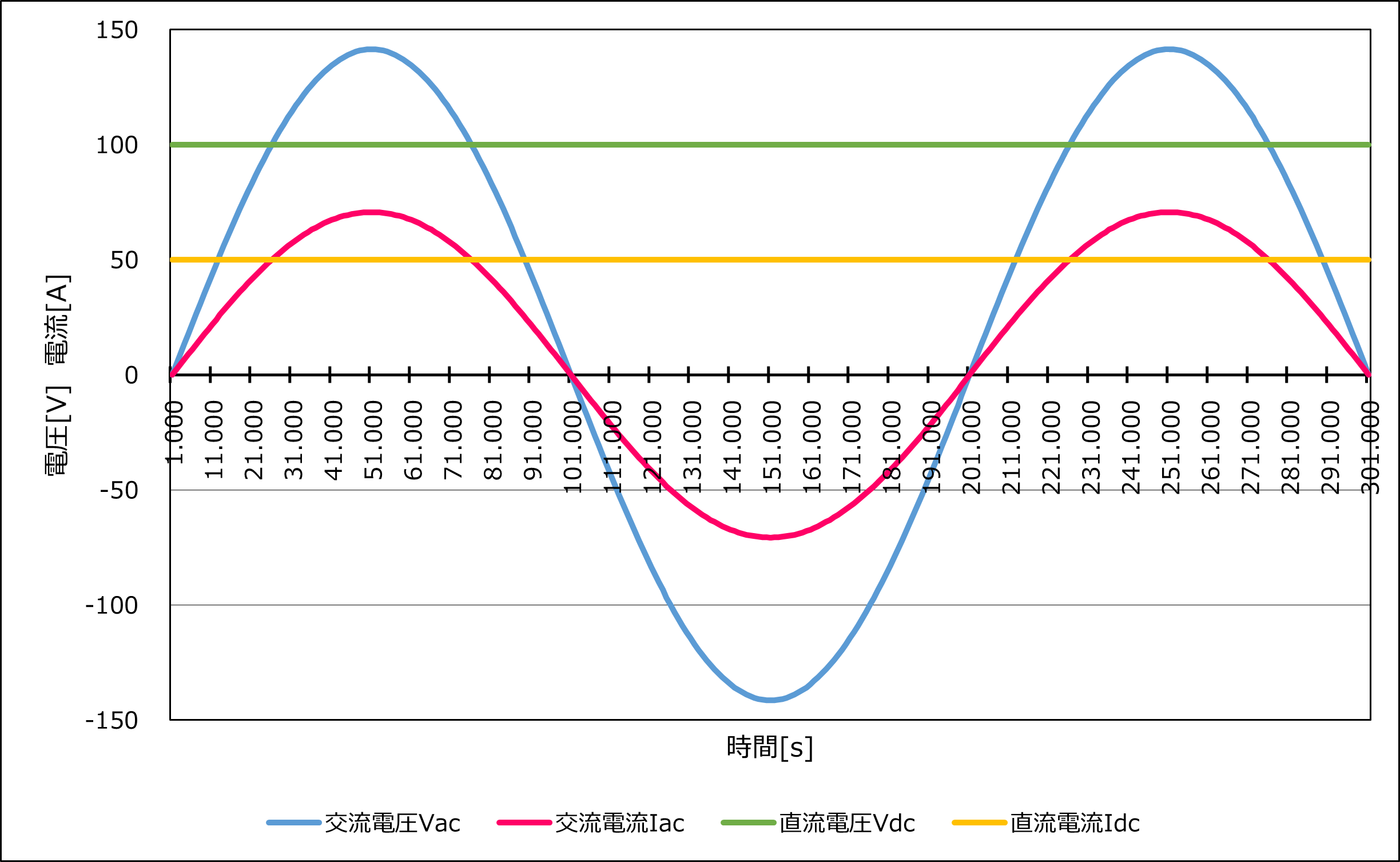
グラフ2は交流電圧Vac=100[V]、交流電流Iac=50[A]と直流電圧Vdc=100[V]、直流電流Idc=50[A]のグラフです。
直流と交流のそれぞれの電力Pは等しく、
P=100[V]×50[A]
=5000[W]
となります。
これをグラフで表すとグラフ3になります。
グラフ3

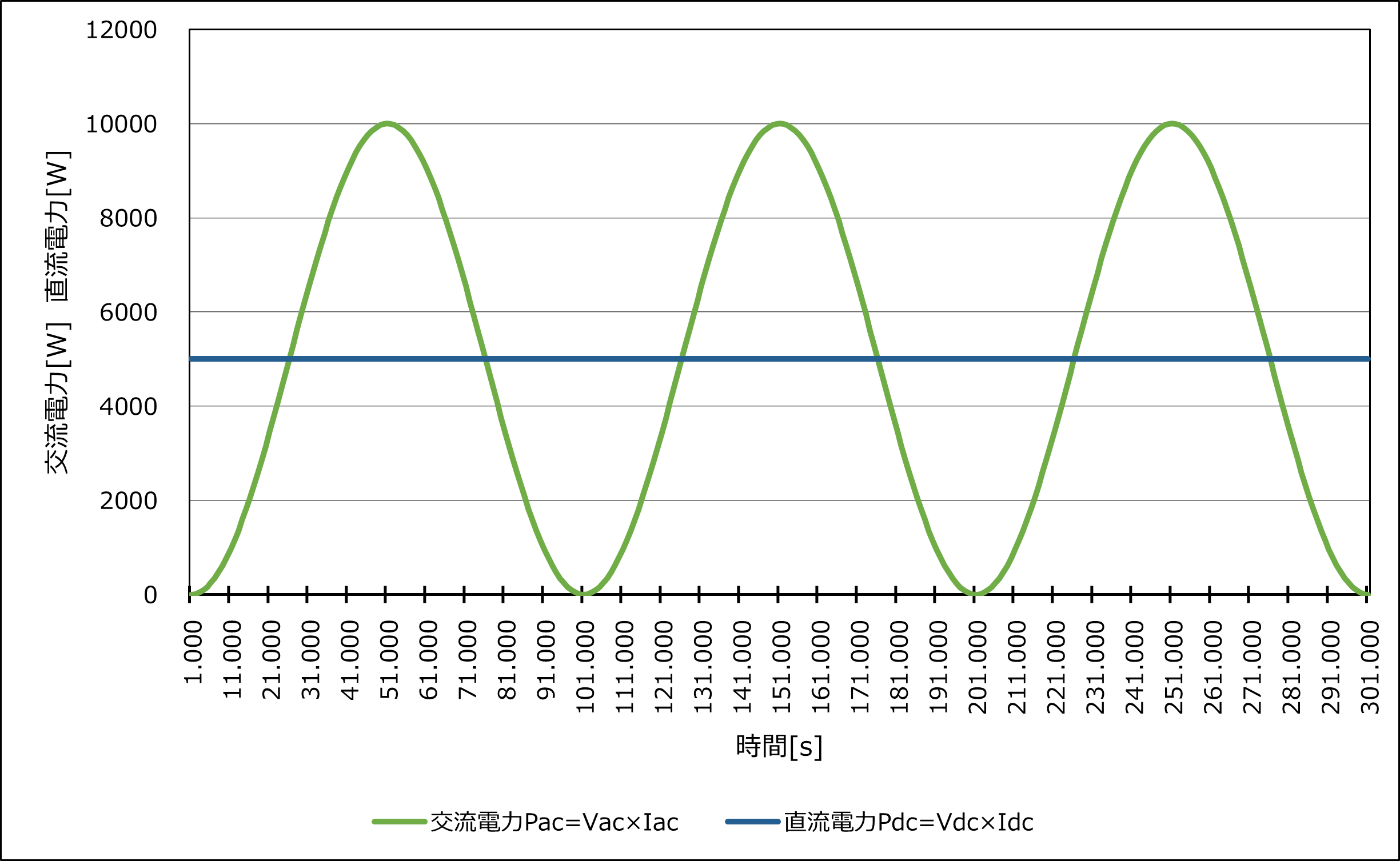
直流電力は、5000[W]になっていて、交流電力の最大値は10000[W]になっています。
交流電力Pacは、
Pac=Vac×Iac
なので
Vac=√2×100×sinωt
と
Iac=√2×50×sinωt
を代入すると
Pac=Vac×Iac
　 =√2×100×sinωt×√2×50×sinωt
　 =2×5000×(sinωt)²
となり、Pacの最大値は5000の2倍になることが分かります。
Pacの最大値は5000の2倍なので、Pacの平均値は最大値の1/2の5000[W]になり、直流電力と等しくなることが分かります。

平均値

正弦波交流は＋と-が入れ替わりますので、1周期分を平均すると0になってしまいます。そこで＋部分の半周期分の平均を平均値といいます。
最大値Imの正弦波交流電流の平均値Iaveは
Iave=2Im/π
となります。

TOPページに戻る
サイト内検索