パーセントインピーダンス法(％インピーダンス法)

パーセントインピーダンス法の考え方

便利なパーセントインピーダンス法

電力系統の短絡容量や電圧降下の計算を行う場合、電路のインピーダンスを合計する必要があります。しかし、電力系統には多数の変圧器があるため、単純にインピーダンスを足し算すると誤った値のインピーダンスになってしまいます。正しく電路のインピーダンスを合計するには、変圧器の2次側のインピーダンスを1次側に換算するという作業を変圧器の台数分繰り返すという、面倒な計算をしなければなりません。それを簡単に計算するためにパーセントインピーダンス法が考えられました。 それでは、パーセントインピーダンス法がなぜ便利なのか、具体的に考えてみます。
図1

図1は100[V]の電源に負荷が接続され、0.1[A]の電流が流れています。 ボックスの中身は見えませんが、変圧器の1次側は、100[V]の電圧がかかっていて、0.1[A]の電流が流れているので、ボックスの中の抵抗はオームの法則より

となります。
図2は、図1のボックスの中身が見える状態にした図です。
図2


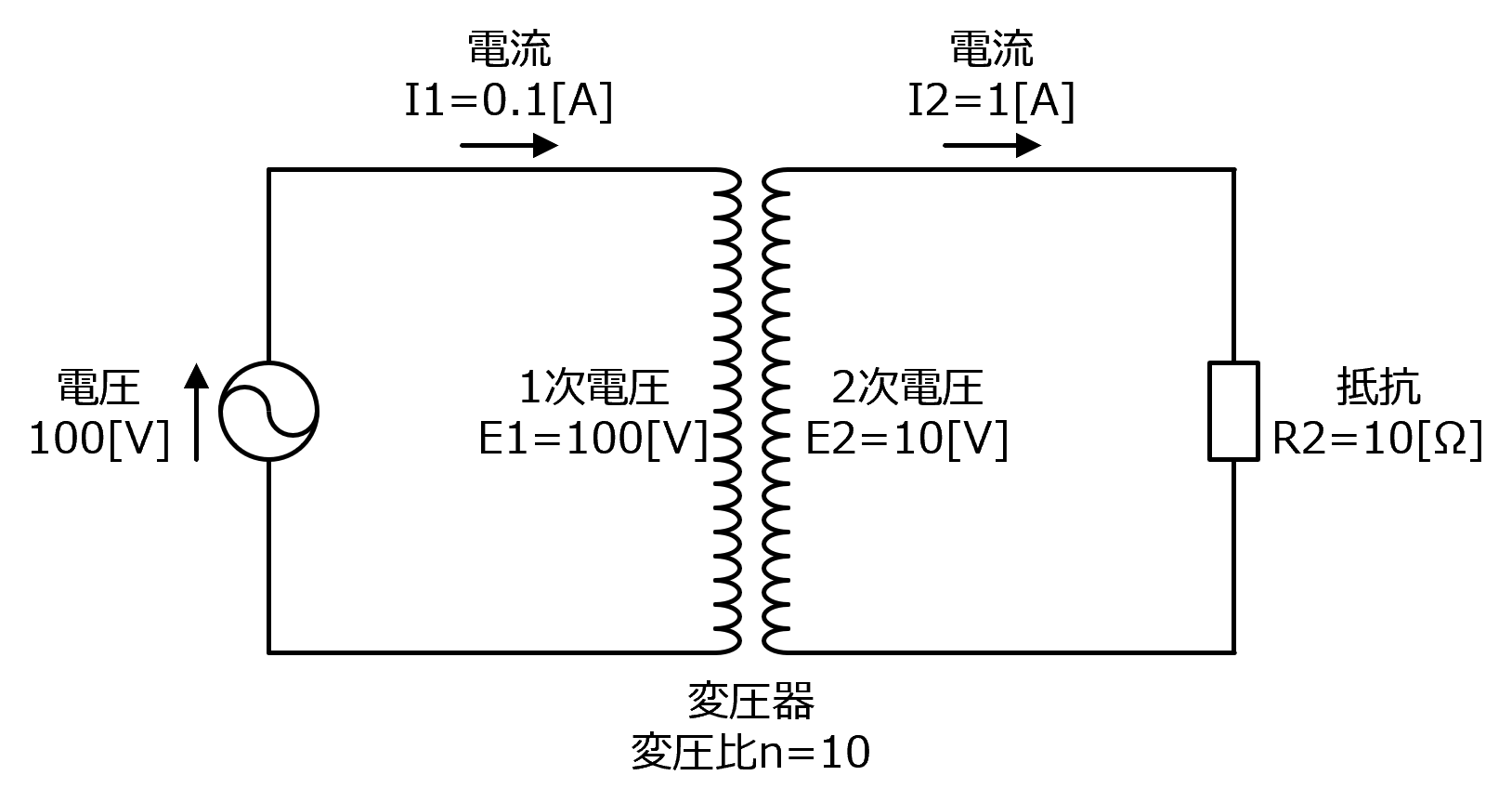
ボックス内には変圧器があり、1次電圧の100[V]を10[V]に変圧していて、変圧器2次側には10[Ω]の抵抗が接続されています。 図1の計算ではボックスの中の抵抗は1000[Ω]という計算結果でしたが、実際には変圧器を経由して10[Ω]の抵抗が接続されていたのです。 これは、変圧器2次側の抵抗を変圧器1次側に換算する場合は変圧比nの2乗で割ってやる必要があるということ表しています。 変電所から需要家までの電力系統には、500kV、275kV、154kV、77kV、33kV、22kV、6.6kVといった様々な電圧階級があり、それぞれの区間には電路や変圧器のインピーダンスが散在しています。例えば6.6kVの部分で短絡したら500kVの部分にはどのくらいの短絡電流が流れるのかを計算する場合、電源から短絡点に至るまでの電路や変圧器のインピーダンスをすべて変圧比で換算して計算するという気の遠くなる作業をしなければいけません。その計算を簡単に行うためにパーセントインピーダンスが考案されました。

パーセントインピーダンスの計算方法

図3は3相電源に負荷が接続されている図です。
図3

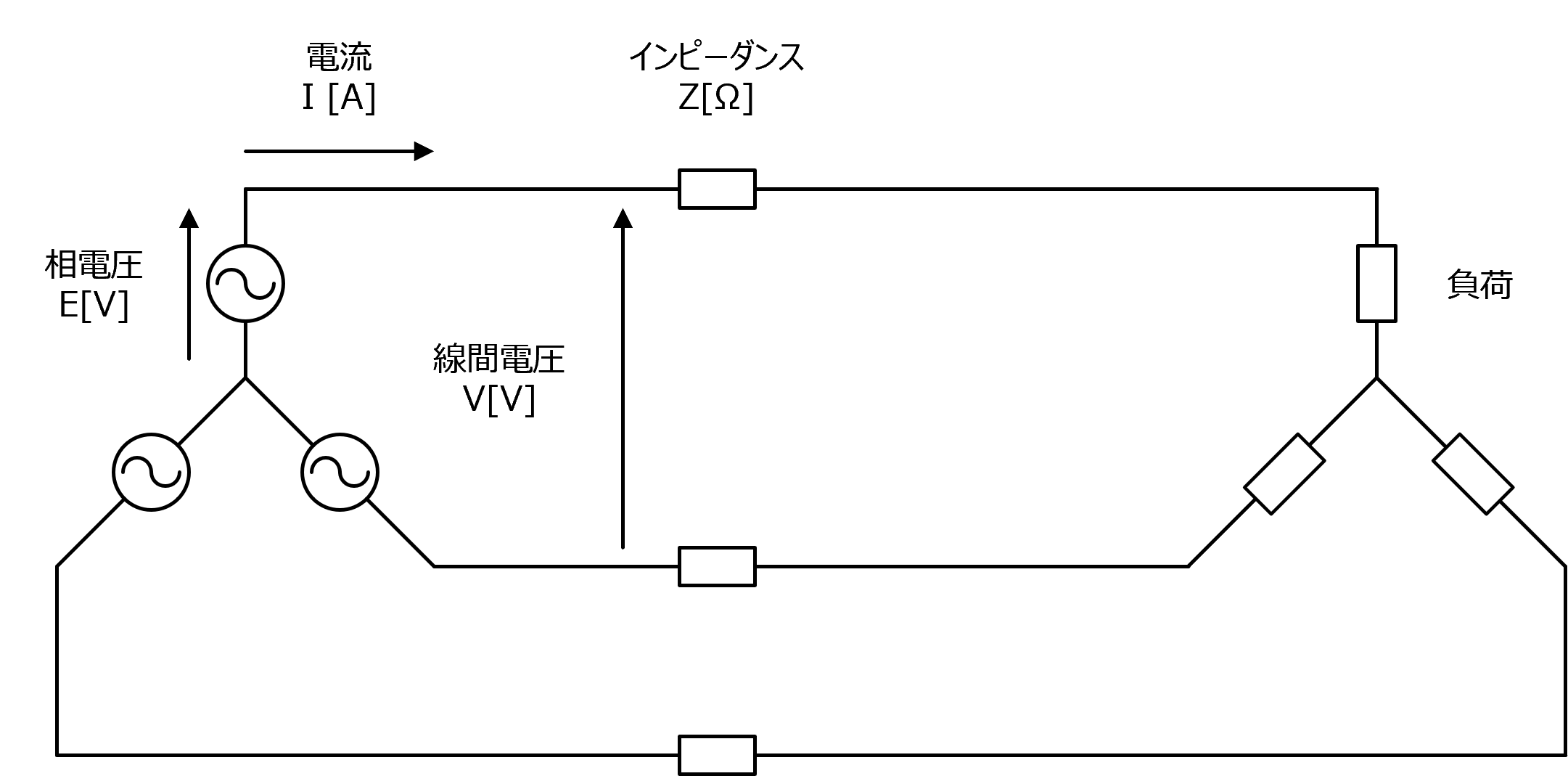
3相回路のままでは計算がややこしいので、単相回路で考えます。 3相の電圧や負荷がすべてバランスしている場合は、3相回路から1相分を切り取って図4のような回路で考えることができます。
図4

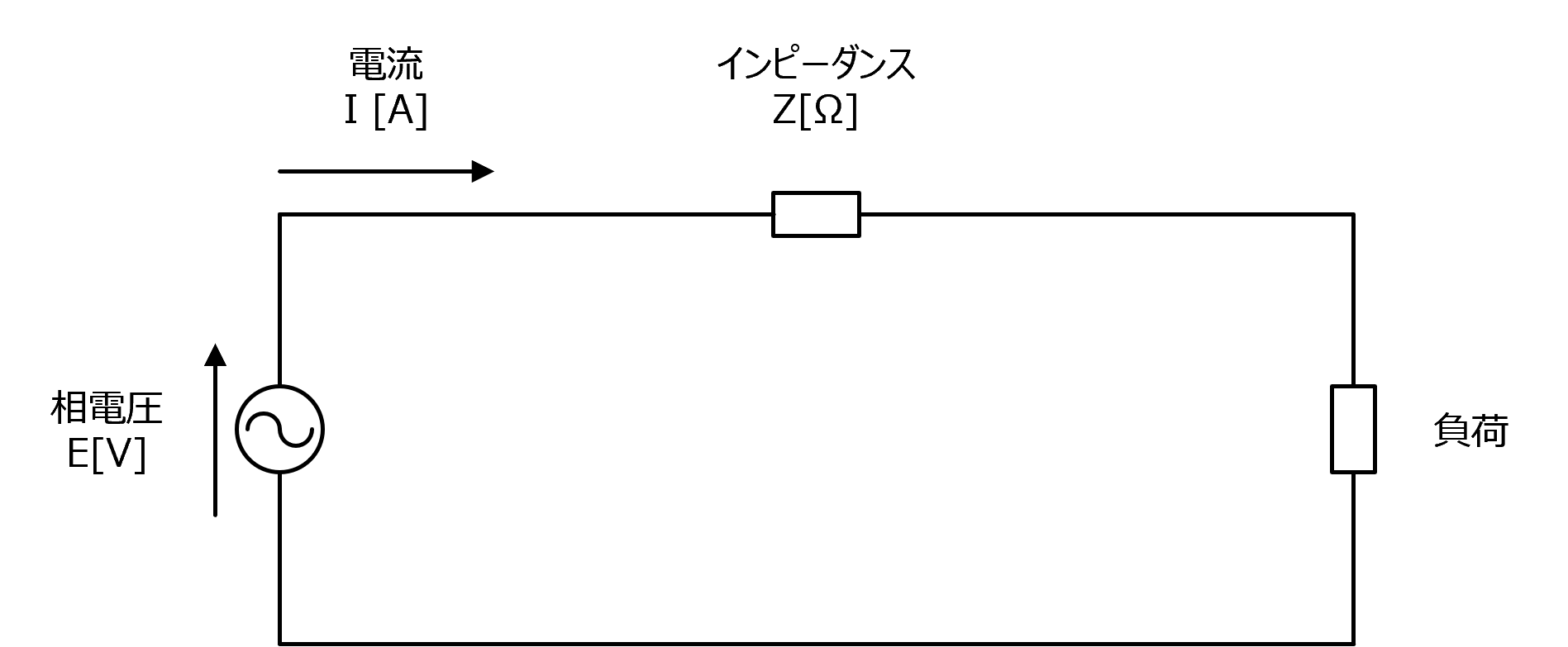
図4のインピーダンスZ[Ω]をパーセントインピーダンスに変換する公式は、

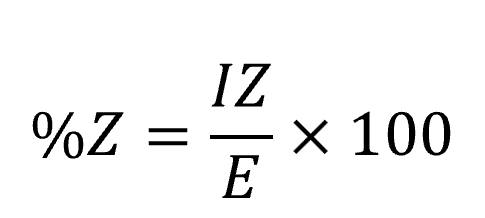
となります。この公式の分母のEは相電圧、分子のIZはケーブルのインピーダンスでの電圧降下ですので、%Zは相電圧のうち何%が電路のインピーダンスで電圧降下しているかという数値であると考えられます。電圧降下はインピーダンスに流れる電流に比例して変化しますので、電流をどのくらい流しているときの電圧降下とするかを決めなればいけません。電力系統のように、発電所から需要家までの間に複数の変圧器があると、その区間によって電流も変化するため、各区間のパーセントインピーダンスを求めるには各区間の電流を求める必要が出てきてしまいます。 そこで、公式から電流Iを消すために下記の変換を行います。

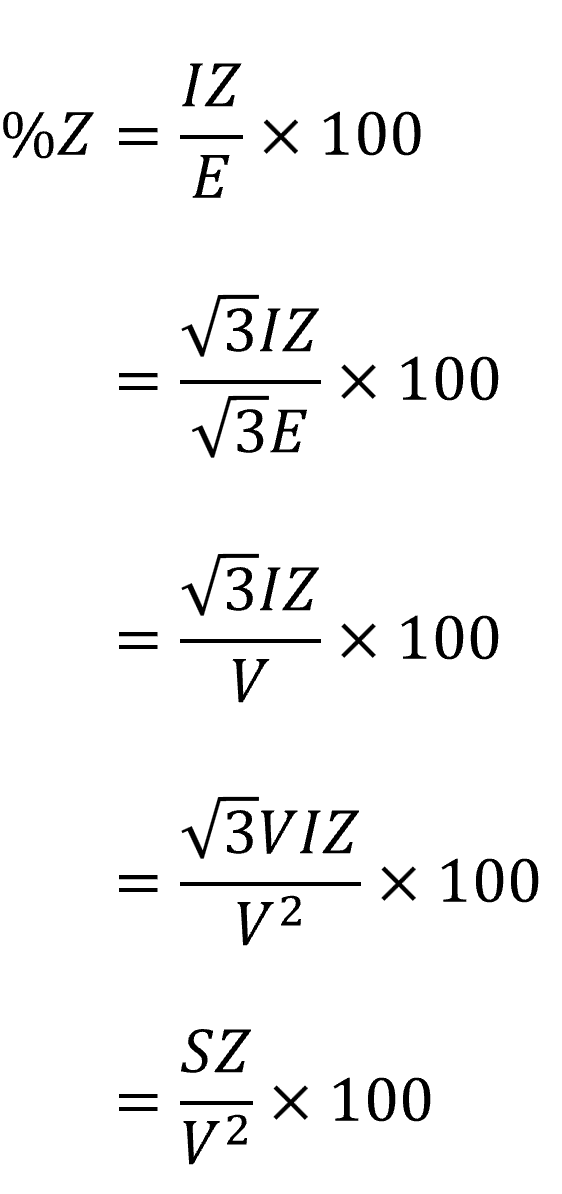
ここで分子に皮相電力S[VA]が出てきました。この皮相電力S[VA]を基準容量といいます。 基準容量は、ひとつの基準容量に統一して計算すれば、計算する人が自由に決められる容量になります。したがって、計算を表す際に「基準容量は○○[VA]とする。」と明記する必要があります。慣習として、特に明記していない場合は基準容量を10[MVA]とすることになっています。変圧器単体のパーセントインピーダンスを計算する場合は、その変圧器の定格容量を基準とすることが多く、これを自己容量基準といいます。 パーセントインピーダンスは電力系統の計算で使用することが多いので、電圧Vの単位は[V]よりも[kV]の方が0の数が減って扱いやすいです。また、基準容量は10[MVA]=10000[kVA]や変圧器容量の○○[kVA]という単位が多いので、皮相電力Sも[VA]より[kVA]の方がよいので、これらを公式に反映します。

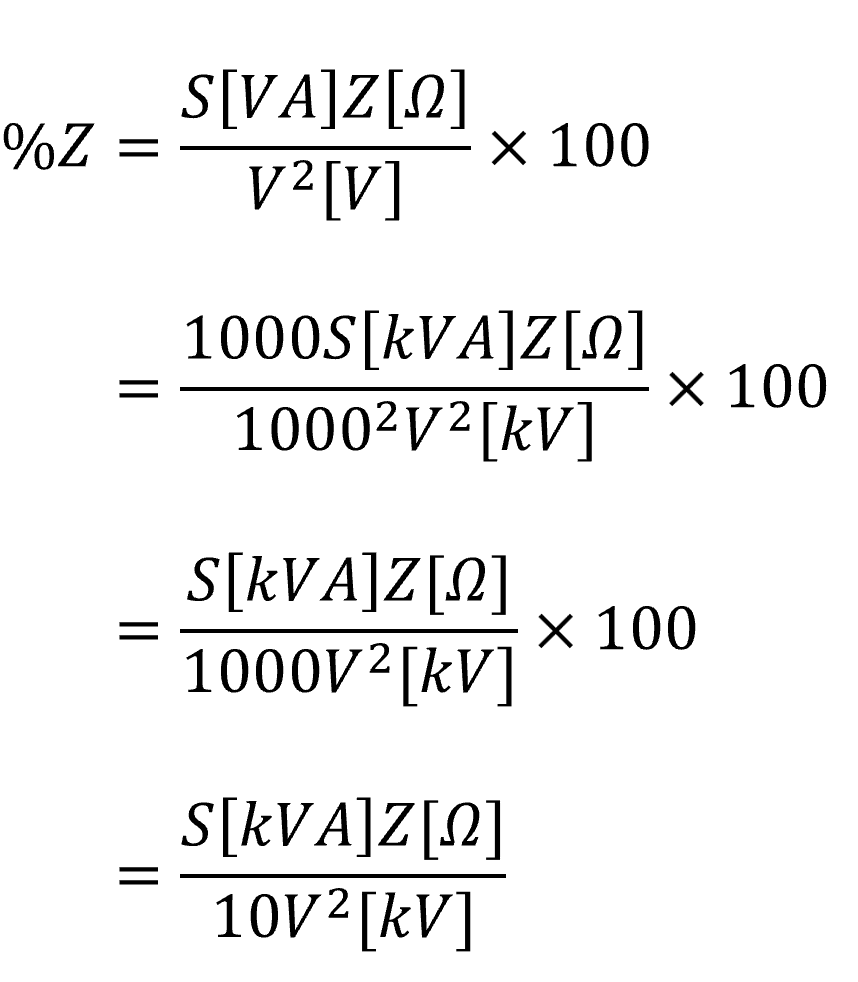
これがパーセントインピーダンスの重要な公式になります。この公式を利用して下記の例題を解いてみます。
【例題】
線間電圧77[kV]の送電系統において、50[Ω]のパーセントインピーダンス[%]を求めよ。ただし、基準容量は10[MVA]とする。
【解答】

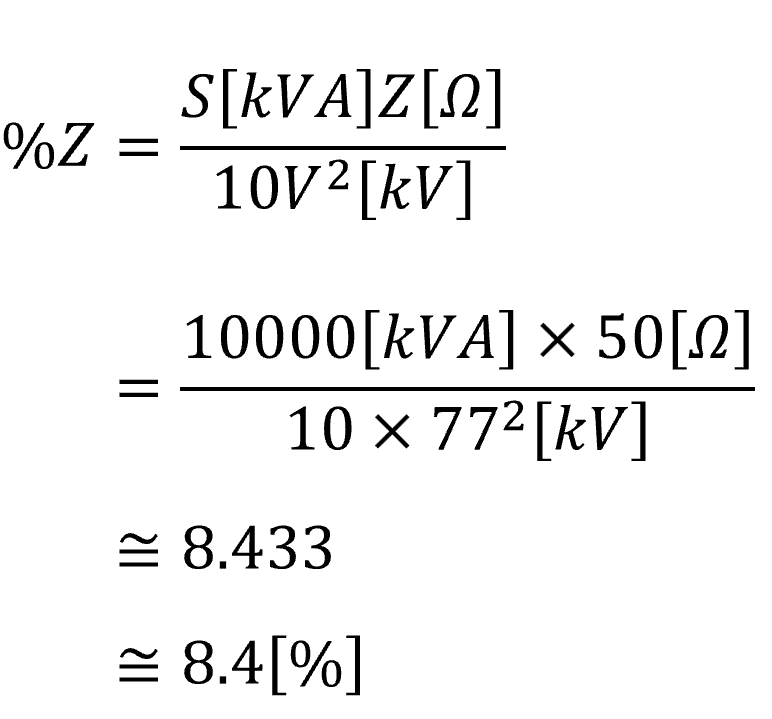
次に、パーセントインピーダンスで計算するメリットがわかる例題を解いてみます。
【例題】
下図の三相3線式配電線路において、22[kV]配電線の末端で三相短絡が発生した場合の電流値を求めよ。ただし、図に記載された定数以外の定数は無視する。

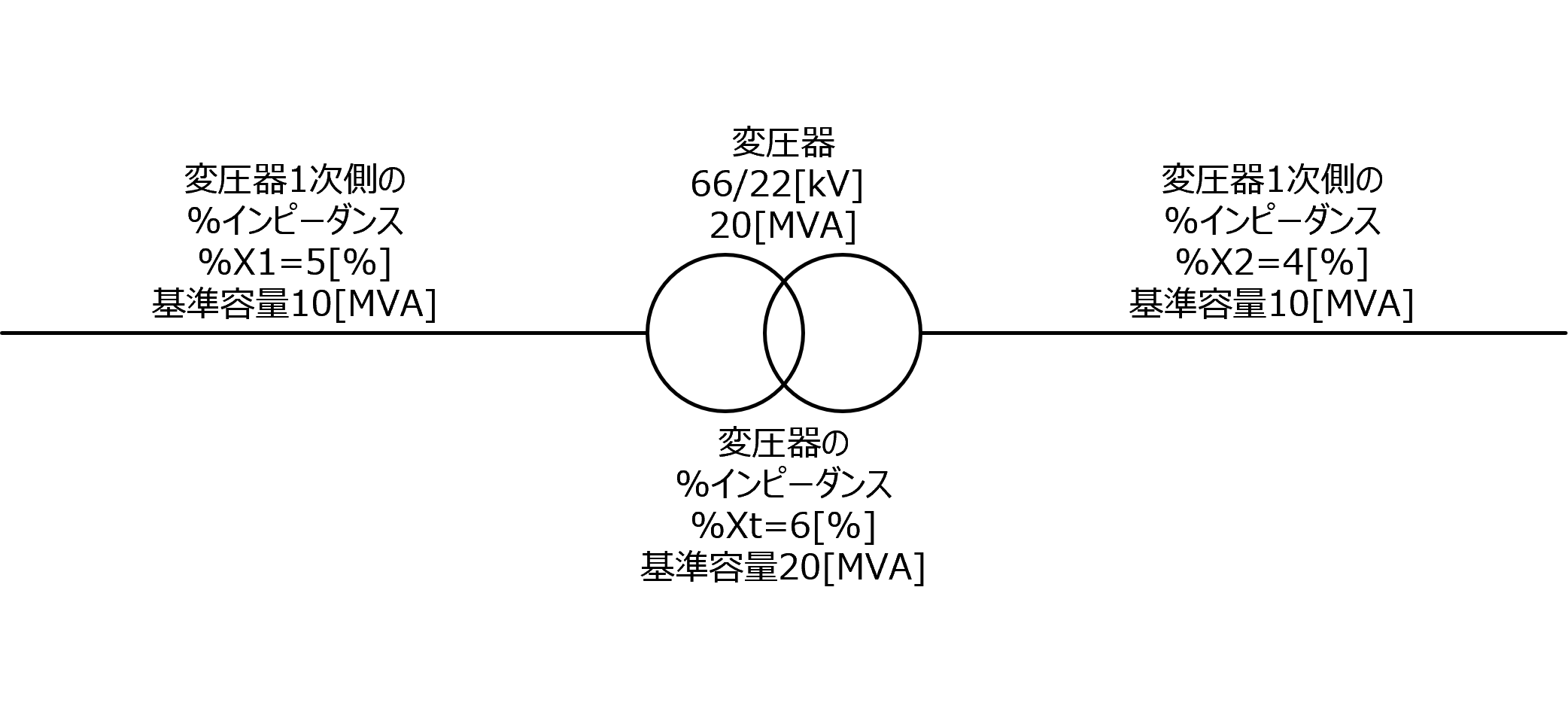
【解答】
変圧器の%インピーダンスを10[MVA]基準に換算する。

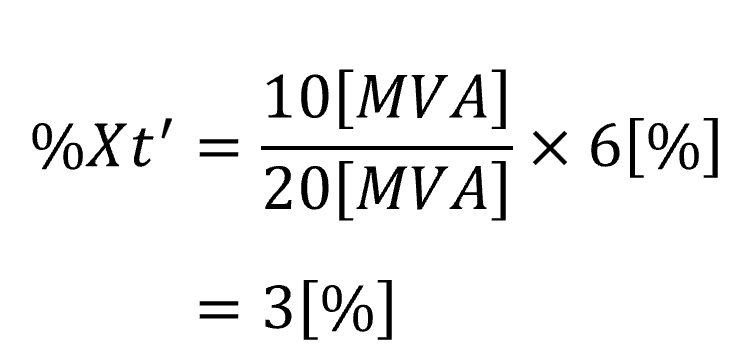
全体の%インピーダンスを求める。

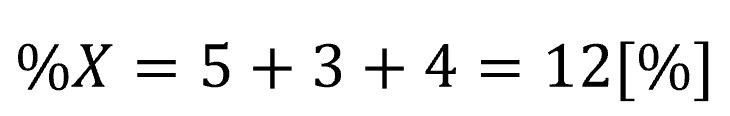
22[kV]におけるインピーダンスを求める。
%インピーダンスで計算すると、この全体のインピーダンスを求める計算が変圧器を気にせずにできて、楽になります。

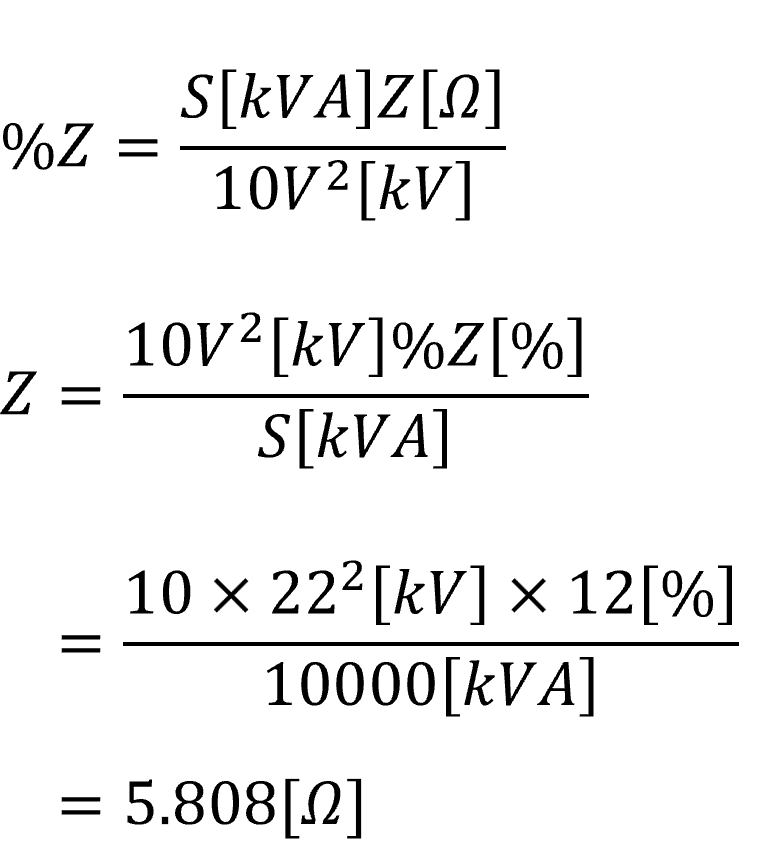
オームの法則で三相短絡電流を求める。

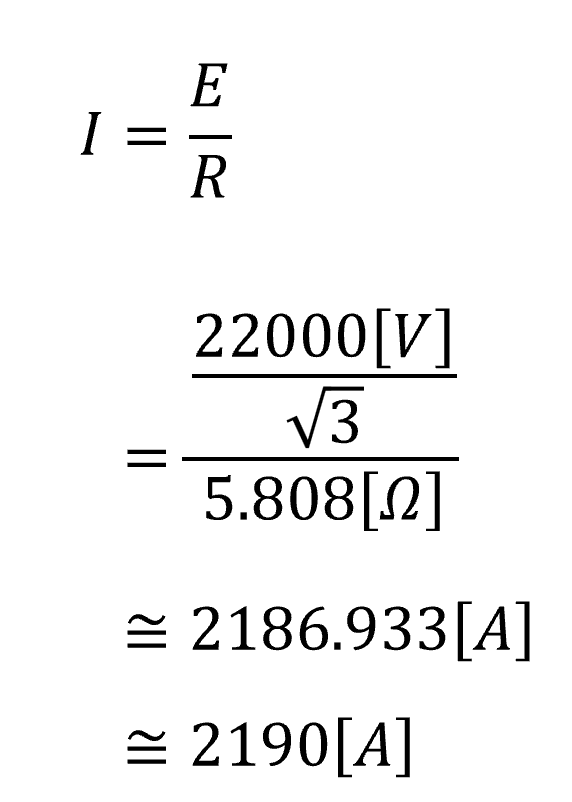
変圧器のパーセントインピーダンス

変圧器の％Zは、10000kVA基準で
6.6kVで約3.5％、22kVで約5.0％、66kVで約7.5％
となっています。しかし、短絡容量を低減させるためにわざと％Zを高く作っている変圧器もあります。これは変圧器を並列接続して運転するとインピーダンスが低くなり、短絡容量が増大するので、電源側の遮断器が大きくなりすぎたり、コストがかかりすぎたりするためです。

TOPページに戻る
サイト内検索